Задача
Из центра каждой из двух данных окружностей проведены касательные к другой окружности.
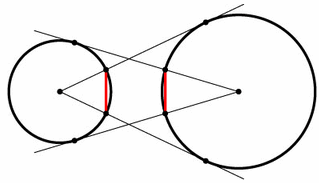
Докажите, что хорды, соединяющие точки пересечения касательных с окружностями, (см. рис.) равны.
Решение
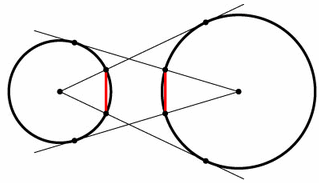
Пусть O1 и O2 – центры окружностей; r и R – их радиусы, AB и CD – указанные хорды; M и N – их точки пересечения с отрезком O1O2; O2P – касательная к первой окружности (P – точка касания). Ясно, что M и N – середины этих хорд.
Из подобия прямоугольных треугольников O2ND и O2PO1 находим, что DC = 2DN = 2O1P·O2D/O1O2 = 2rR/O1O2. Аналогично AB = 2rR/O1O2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет