Задача
Из произвольной точки M внутри равностороннего треугольника опущены перпендикуляры MK1, MK2, MK3 на его стороны. Докажите, что
$\displaystyle \overrightarrow{MK_{1}}$ + $\displaystyle \overrightarrow{MK_{2}}$ + $\displaystyle \overrightarrow{MK_{3}}$ = $\displaystyle {\textstyle\frac{3}{2}}$ . $\displaystyle \overrightarrow{MO}$,
гдеO— центр треугольника.
Решение
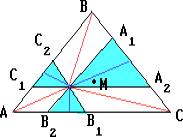
Проведем через точку M прямые, параллельные сторонам треугольника, и обозначим точки пересечения этих прямых со сторонами треугольника, как показано на рисунке. Тогда K1, K2, K3 -- середины отрезков A1A2, B1B2, C1C2 соответственно. Поэтому
$\displaystyle \overrightarrow{MK_{1}}$ = $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \overrightarrow{MA_{1}}$ + $\displaystyle \overrightarrow{MA_{2}}$), $\displaystyle \overrightarrow{MK_{2}}$ = $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \overrightarrow{MB_{1}}$ + $\displaystyle \overrightarrow{MB_{2}}$), $\displaystyle \overrightarrow{MK_{3}}$ = $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \overrightarrow{MC_{1}}$ + $\displaystyle \overrightarrow{MC_{2}}$).
Кроме того,
$\displaystyle \overrightarrow{MC_{1}}$ + $\displaystyle \overrightarrow{MB_{2}}$ = $\displaystyle \overrightarrow{MA}$, $\displaystyle \overrightarrow{MC_{2}}$ + $\displaystyle \overrightarrow{MA_{1}}$ = $\displaystyle \overrightarrow{MB}$, $\displaystyle \overrightarrow{MA_{2}}$ + $\displaystyle \overrightarrow{MB_{1}}$ = $\displaystyle \overrightarrow{MC}$.
Тогда
$\displaystyle \overrightarrow{MK_{1}}$ + $\displaystyle \overrightarrow{MK_{2}}$ + $\displaystyle \overrightarrow{MK_{3}}$ = $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \overrightarrow{MA_{1}}$ + $\displaystyle \overrightarrow{MA_{2}}$ + $\displaystyle \overrightarrow{MB_{1}}$ + $\displaystyle \overrightarrow{MB_{2}}$ + $\displaystyle \overrightarrow{MC_{1}}$ + $\displaystyle \overrightarrow{MC_{2}}$) =
= $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \left(\vphantom{(\overrightarrow{MC_{1}} + \overrightarrow{MB_{2}...
...htarrow{MA_{1}})
+ (\overrightarrow{MA_{2}} + \overrightarrow{MB_{1}})}\right.$($\displaystyle \overrightarrow{MC_{1}}$ + $\displaystyle \overrightarrow{MB_{2}}$) + ($\displaystyle \overrightarrow{MC_{2}}$ + $\displaystyle \overrightarrow{MA_{1}}$) + ($\displaystyle \overrightarrow{MA_{2}}$ + $\displaystyle \overrightarrow{MB_{1}}$)$\displaystyle \left.\vphantom{(\overrightarrow{MC_{1}} + \overrightarrow{MB_{2}...
...htarrow{MA_{1}})
+ (\overrightarrow{MA_{2}} + \overrightarrow{MB_{1}})}\right)$ =
= $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \overrightarrow{MA}$ + $\displaystyle \overrightarrow{MB}$ + $\displaystyle \overrightarrow{MC}$) = $\displaystyle {\textstyle\frac{1}{2}}$ . 3 . $\displaystyle \overrightarrow{MO}$ = $\displaystyle {\textstyle\frac{3}{2}}$$\displaystyle \overrightarrow{MO}$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет