Задача
Существуют ли две трапеции, основания первой из которых соответственно равны боковым сторонам второй, а основания второй — боковым сторонам первой?
Решение
Через вершину B меньшего основания BC трапеции ABCD проведём прямую, параллельную боковой стороне CD. Пусть эта прямая пересекает основание AD в точке K. В треугольнике ABK
AK = AD - DK = AD - BC, BK = CD,
т.к.BCDK— параллелограмм. Тогда
AD - BC > | AB - BK| = | AB - CD|,
т.е. в любой трапеции разность оснований больше разности боковых
сторон. Отсюда следует утверждение задачи.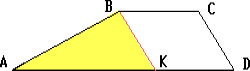
Ответ
Нет.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет