Задача
На диаметре AC некоторой окружности дана точка E. Проведите через неё хорду BD так, чтобы площадь четырёхугольника ABCD была наибольшей.
Решение
Пусть O — центр, R — радиус окружности, OE = a (рис.1). Тогда
SABCD = S$\scriptstyle \Delta$ADC + S$\scriptstyle \Delta$ABC = $\displaystyle {\frac{2R}{a}}$S$\scriptstyle \Delta$ODE + $\displaystyle {\frac{2R}{a}}$S$\scriptstyle \Delta$OBE =
= $\displaystyle {\frac{2R}{a}}$(S$\scriptstyle \Delta$ODE + S$\scriptstyle \Delta$OBE) = $\displaystyle {\frac{2R}{a}}$S$\scriptstyle \Delta$OBD.
Следовательно, площадь четырёхугольникаABCDнаибольшая, когда
наибольшая площадь треугольникаOBD.
Треугольник OBD — равнобедренный,
OB = OD = R, S$\scriptstyle \Delta$OBD = $\displaystyle {\textstyle\frac{1}{2}}$R2sin$\displaystyle \varphi$,
где$\varphi$=$\angle$BOD.
Угол$\varphi$тем меньше, чем меньше хордаBD, или чем длиннее
проведённый к этой хорде перпендикулярOH.
Поскольку
OH $\leqslant$ OE = a, то наименьшее значение
$\varphi$ = $\varphi_{0}^{}$
характеризуется тем, что отрезки OH и OE совпадают, что
соответствует хорде BD, перпендикулярной AC. В этом случае
cos${\frac{\varphi _{0}}{2}}$ = ${\frac{a}{R}}$.
Итак, остается найти наибольшее значение площади треугольника OBD при $\varphi_{0}^{}$ $\leqslant$ $\varphi$ < $\pi$. Возможны следующие два случая.
- Если $\varphi_{0}^{}$ $\leqslant$ ${\frac{\pi}{2}}$, то максимум достигается при
$\varphi$ = ${\frac{\pi}{2}}$. В этом случае
$\displaystyle {\frac{a}{R}}$ = cos$\displaystyle {\frac{\varphi_{0}}{2}}$ $\displaystyle \geqslant$ cos$\displaystyle {\frac{\pi}{4}}$ = $\displaystyle {\frac{\sqrt{2}}{2}}$, a $\displaystyle \geqslant$ $\displaystyle {\frac{R}{\sqrt{2}}}$,
а искомая хордаBD, стягивающая дугу в90o, должна отстоять от
центра на расстояние${\frac{R}{\sqrt{2}}}$, т.е. должна касаться окружности с
центромOрадиуса${\frac{R}{\sqrt{2}}}$.
2) Если же
$\varphi_{0}^{}$ > ${\frac{\pi}{2}}$ (что будет при
a < ${\frac{R}{\sqrt{2}}}$), то максимум
площади достигается при
$\varphi$ = $\varphi_{0}^{}$. В этом случае искомая хорда BD
должна быть перпендикулярна диаметру AC.
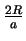
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет