Задача
Две стороны треугольника равны 10 и 15. Докажите, что биссектриса угла между ними не больше 12.
Решение
Первый способ.
Обозначим стороны BC и AC треугольника ABC через a и b
соответственно, а его биссектрису CD — через x (в данном случае
a = 10, b = 15).
Через точку D проведём прямую, параллельную стороне BC, до пересечения со стороной AC в точке M (рис.1). Тогда
$\displaystyle \angle$MDC = $\displaystyle \angle$BCD = $\displaystyle \angle$DCM.
Поэтому треугольникDCM— равнобедренный.
Из подобия треугольниковADMиABCнаходим, что
DM = BC . $\displaystyle {\frac{AD}{AB}}$ = $\displaystyle {\frac{ab}{a+b}}$
(т.к.${\frac{AD}{BD}}$=${\frac{AC}{BC}}$=${\frac{b}{a}}$). Следовательно,
x = CD < CM + DM = 2DM = $\displaystyle {\frac{2ab}{a+b}}$ = 2 . 10 . $\displaystyle {\frac{15}{10+15}}$ = 12.
Второй способ.
Обозначим стороны BC и AC треугольника ABC через a и b
соответственно, а его биссектрису CD — через x (в данном случае
a = 10, b = 15). По свойству биссектрисы треугольника
$\displaystyle {\frac{BD}{DA}}$ = $\displaystyle {\frac{BC}{AC}}$ = $\displaystyle {\frac{a}{b}}$.
Через точкиBиDпроведём прямые, перпендикулярные
биссектрисеCD, до пересечения с прямойACв точкахKиLсоответственно (рис.2). Тогда треугольникBCK— равнобедренный
(его высота и биссектриса, проведённые из вершиныC, совпадают).
Поэтому
AK = AC - CK = AC - BC = b - a, $\displaystyle {\frac{KL}{LA}}$ = $\displaystyle {\frac{BD}{DA}}$ = $\displaystyle {\frac{a}{b}}$.
Следовательно,
KL = AK . $\displaystyle {\frac{a}{a+b}}$ = $\displaystyle {\frac{a(b-a)}{a+b}}$,
CL = CK + KL = CB + KL = a + $\displaystyle {\frac{a(b-a)}{a+b}}$ = $\displaystyle {\frac{2ab}{a+b}}$ = 2 . 10 . $\displaystyle {\frac{15}{10+15}}$ = 12,
x = CD < CL = 12.
Третий способ.
Обозначим стороны BC и AC треугольника ABC через a и b
соответственно, а его биссектрису CD — через x (в данном случае
a = 10, b = 15),
$\angle$ACB = 2$\alpha$ (рис.3). Тогда
x = $\displaystyle {\frac{2ab\cos \alpha}{a+b}}$.
Следовательно,
СВ = x < $\displaystyle {\frac{2ab}{a+b}}$ = 2 . 10 . $\displaystyle {\frac{15}{10+15}}$ = 12.
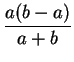
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет