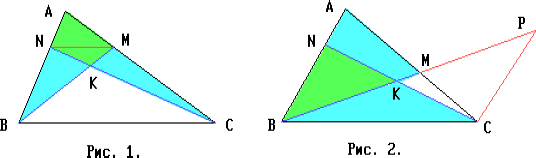
Пусть точки M и N расположены соответственно на сторонах AC
и AB треугольника ABC, K — точка пересечения отрезков BM
и CN. Докажем, что три полученных треугольника BKN, BKC и
CKM не могут быть равновеликими.
Предположим, что
S$\scriptstyle \Delta$BKN = S$\scriptstyle \Delta$BKC = S$\scriptstyle \Delta$CKM.
Тогда точка K — середина CN и BM. Следовательно, четырёхугольник
BNMC — параллелограмм, т.е.
BN || CM, что невозможно.
Пусть
SAMKN = S$\scriptstyle \Delta$BKN = S$\scriptstyle \Delta$CKM = s. Высоты
равновеликих треугольников BNC и BMC, проведённые из вершин N
и M равны, поэтому
NM || BC.
Обозначим
$\displaystyle {\frac{AN}{AB}}$ = $\displaystyle {\frac{AM}{AC}}$ = $\displaystyle {\frac{NM}{BC}}$ = $\displaystyle {\frac{MK}{KB}}$ = x.
Тогда
$\displaystyle {\textstyle\frac{1}{2}}$ = $\displaystyle {\frac{S_{\Delta BKN}}{S_{\Delta BMA}}}$ = $\displaystyle {\frac{BN}{AB}}$ . $\displaystyle {\frac{BK}{BM}}$ = (1 - x) . $\displaystyle {\frac{1}{1+x}}$ = $\displaystyle {\frac{1-x}{1+x}}$.
Отсюда находим, что
x=${\frac{1}{3}}$. Следовательно,
S$\scriptstyle \Delta$BKC = $\displaystyle {\frac{CK}{KN}}$S$\scriptstyle \Delta$BKN = 3s.
Легко проверить, что если${\frac{AN}{AB}}$=${\frac{AM}{AC}}$=${\frac{1}{3}}$, то
SAMKN = S$\scriptstyle \Delta$BKN = S$\scriptstyle \Delta$CKM.
Пусть теперь
SAMKN =
S$\scriptstyle \Delta$BKN =
S$\scriptstyle \Delta$BKC =
s. Если
S$\scriptstyle \Delta$CKM =
q, то
$\displaystyle {\frac{AN}{BN}}$ = $\displaystyle {\frac{S_{\Delta ACN}}{S_{\Delta BCN}}}$ = $\displaystyle {\frac{s + q}{2s}}$, $\displaystyle {\frac{BK}{KM}}$ = $\displaystyle {\frac{S_{\Delta BKC}}{S_{\Delta CKM}}}$ = $\displaystyle {\frac{BK}{KM}}$ = $\displaystyle {\frac{s}{q}}$.
Следовательно,
$\displaystyle {\textstyle\frac{1}{2}}$ = $\displaystyle {\frac{BN}{AB}}$ . $\displaystyle {\frac{BK}{BM}}$ = $\displaystyle {\frac{2s}{3s+q}}$ . $\displaystyle {\frac{s}{s+q}}$.
После упрощения получим квадратное уравнение
q2 + 4sq - s2 = 0,
из которого находим, что
q=
s($\sqrt{5}$- 2).
Докажем теперь, что если точка
N на стороне
AB треугольника
ABC такова, что
${\frac{AN}{NB}}$ = ${\frac{\sqrt{5} - 1}{2}}$, а точка
K — середина
отрезка
CN, то
SAMKN =
S$\scriptstyle \Delta$BKN =
S$\scriptstyle \Delta$BKC.
Пусть прямая BK пересекает сторону AC в точке M. Через
вершину C проведём прямую, параллельную стороне AB, до
пересечения с прямой BK в точке P. Из равенства треугольников
PKC и BKN следует, что PC = BN, а из подобия треугольников PMC и
BMA —
$\displaystyle {\frac{AM}{MC}}$ = $\displaystyle {\frac{AB}{PC}}$ = $\displaystyle {\frac{AB}{BN}}$ = $\displaystyle {\frac{\sqrt{5} + 1}{2}}$.
С помощью аналогичных рассуждений найдём, что
$\displaystyle {\frac{BK}{KM}}$ = $\displaystyle {\frac{1}{\sqrt{5} - 2}}$.
Следовательно,
$\displaystyle {\frac{S_{\Delta BKN}}{S_{\Delta BMA}}}$ = $\displaystyle {\frac{BN}{AB}}$ . $\displaystyle {\frac{BK}{BM}}$ = $\displaystyle {\frac{2}{\sqrt{5} + 1}}$ . $\displaystyle {\frac{1}{\sqrt{5} - 1}}$ = $\displaystyle {\textstyle\frac{1}{2}}$.
Таким образом,
SAMKN=
S$\scriptstyle \Delta$BKN=
S$\scriptstyle \Delta$BKC.
Аналогично для случая, когда
SAMKN = S$\scriptstyle \Delta$BKC = S$\scriptstyle \Delta$CKN.