Задача
Пользуясь только циркулем, разделите пополам данный отрезок, то есть постройте для данных точек A и B такую точку C, что точки A, B, C лежат на одной прямой и AC = BC.
Решение
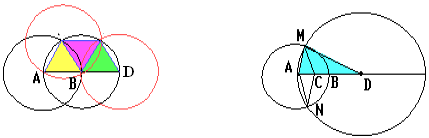
Как в задаче 158333 а) удвоим отрезок AB, то есть построим точку D, для которой AD = 2AB и точки A, B, D лежат на одной прямой (B между A и D) (рис. слева).
Затем построим окружность с центром D и радиусом DA. Пусть M и N – точки её пересечения с уже построенной окружностью с центром A радиуса AB. С центрами в точках M и N построим окружности радиуса MA = NA. Их точка пересечения, отличная от A, есть искомая середина отрезка AB.
Действительно, точки A, C и D лежат на одной прямой, так как каждая из них равноудалена от концов отрезка MN, то есть лежит на серединном перпендикуляре к этому отрезку. С другой стороны, из подобия равнобедренных треугольников AMC и ADM следует, что AC : AB = AM : AD = 1 : 2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь