Задача
Найдите геометрическое место точек, расстояния от каждой из которых до двух данных точек относятся как m : n.
Решение
Первый способ.
Рассмотрим случай, когда m$\ne$n. Пусть A и B — данные точки.
Пусть точка P такова, что
${\frac{PA}{PB}}$ = ${\frac{m}{n}}$. Если точка
P не лежит на прямой AB, то проведём биссектрису PC треугольника
APB и биссектрису внешнего угла треугольника APB, смежного с углом
APB, до пересечения с прямой AB в точке C1.
Тогда
$\displaystyle {\frac{AC}{BC}}$ = $\displaystyle {\frac{AC_{1}}{BC_{1}}}$ = $\displaystyle {\frac{AP}{BP}}$ = $\displaystyle {\frac{m}{n}}$,
а уголCPC1— прямой как угол между биссектрисами смежных углов.
Следовательно, точкаPлежит на окружности с диаметромCC1.
Пусть теперь M — произвольная точка построенной окружности,
отличная от A и B (для которых все и так ясно). Тогда
$\angle$CMC1 = 90o. Проведём через точку B прямую, параллельную AM.
Пусть K и L — точки пересечения проведённой прямой с прямыми MC1 и MC.
Из подобия треугольников BKC1 и AMC1 следует, что
$\displaystyle {\frac{AM}{BK}}$ = $\displaystyle {\frac{AC_{1}}{BC_{1}}}$ = $\displaystyle {\frac{m}{n}}$,
а из подобия треугольниковBLCиAMC—
$\displaystyle {\frac{AM}{BL}}$ = $\displaystyle {\frac{AC}{CB}}$ = $\displaystyle {\frac{m}{n}}$.
Из полученных равенств следует, чтоBK=BL. ПоэтомуMB—
медиана прямоугольного треугольникаKMLс прямым углом при
вершинеM. Следовательно,
MB = BK, $\displaystyle {\frac{AM}{MB}}$ = $\displaystyle {\frac{AM}{BK}}$ = $\displaystyle {\frac{m}{n}}$,
что и требовалось доказать.
Второй способ.
Введём систему координат на плоскости так, чтобы точки A и B
имели координаты (- a;0) и (a;0) соответственно. Если точка P
имеет координаты (x;y), то
$\displaystyle {\frac{AP^{2}}{BP^{2}}}$ = $\displaystyle {\frac{(x + a)^{2} + y^{2}}{(x - a)^{2} + y^{2}}}$.
Уравнение${\frac{AP^{2}}{BP^{2}}}$=${\frac{m^{2}}{n^{2}}}$приводится к виду
$\displaystyle \left(\vphantom{x + \frac{a(m^{2} + n^{2})}{n^{2} - m^{2}}}\right.$x + $\displaystyle {\frac{a(m^{2} + n^{2})}{n^{2} - m^{2}}}$$\displaystyle \left.\vphantom{x + \frac{a(m^{2} + n^{2})}{n^{2} - m^{2}}}\right)^{2}_{}$ + y2 = $\displaystyle \left(\vphantom{\frac{2mn}{n^{2} - m^{2}}}\right.$$\displaystyle {\frac{2mn}{n^{2} - m^{2}}}$$\displaystyle \left.\vphantom{\frac{2mn}{n^{2} - m^{2}}}\right)^{2}_{}$.
Это уравнение окружности с центром$\left(\vphantom{\frac{a(m^{2} + n^{2})}{m^{2} - n^{2}}; 0}\right.$${\frac{a(m^{2} + n^{2})}{m^{2} - n^{2}}}$;0$\left.\vphantom{\frac{a(m^{2} + n^{2})}{m^{2} - n^{2}}; 0}\right)$и радиусом${\frac{2mn}{\vert m^{2} - n^{2}\vert}}$.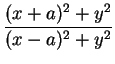
Ответ
Окружность, если m$\ne$n. Если m = n, то искомое геометрическое место точек есть серединный перпендикуляр к отрезку с концами в данных точках.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет