Задача
Высота трапеции, диагонали которой взаимно перпендикулярны, равна 4. Найдите площадь трапеции, если известно, что одна из её диагоналей равна 5.
Решение
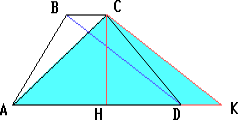
Пусть диагональ BD трапеции ABCD равна 5. Через вершину C основания BC проведем прямую, параллельную диагонали BD, до пересечения с прямой AD в точке K. Тогда ACK — прямоугольный треугольник, CK = BD = 5.
Пусть H — проекция вершины C на прямую AD. По теореме Пифагора
HK = $\displaystyle \sqrt{CK^{2}- CH^{2}}$ = $\displaystyle \sqrt{25 - 16}$ = 3.
Из подобия треугольниковACHиCKHследует, что
AC = $\displaystyle {\frac{CK\cdot CH}{HK}}$ = $\displaystyle {\textstyle\frac{20}{3}}$.
Следовательно,
SABCD = S$\scriptstyle \Delta$ACK = $\displaystyle {\textstyle\frac{1}{2}}$AC . CK = $\displaystyle {\textstyle\frac{50}{3}}$.
Ответ
${\frac{50}{3}}$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет