Задача
Через точку, взятую внутри произвольного треугольника, параллельно его сторонам проведены отрезки с концами на сторонах треугольника.
Докажите, что сумма трёх отношений этих отрезков к параллельным им сторонам треугольника равна 2.
Решение
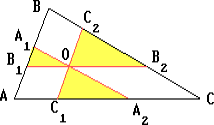
Пусть O – произвольная точка, взятая внутри треугольника ABC; A1A2 || BC, B1B2 || AC, C1C2 || AB (см. рис.). Обозначим A2C = OB2 = x, A2C1 = y,
AC1 = OB1 = z. Тогда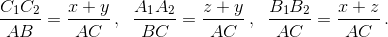 
Поэтому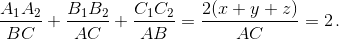 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет