Задача
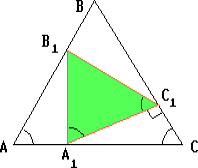
Равнобедренные треугольники ABC (AB = BC) и A1B1C1 (A1B1 = B1C1) подобны и AB : A1B1 = 2 : 1. Вершины A1, B1 и C1 расположены соответственно на сторонах CA, AB и BC, причём A1B1 ⊥ AC. Найдите угол B.
Решение
Пусть A1B1 = B1C1 = 1, ∠A = α. Тогда ∠A1C1C = (90° – α) + α = 90°, AA1 = ctg α, A1C1 = 2 cosα, AC = 2A1C1 = 4 cosα, A1C = A1C1/sin α = 2ctg α.
Так как AC = AA1 + A1C, то 3ctg α = 4cos α, то есть sin α = ¾, откуда cos∠B = cos(180° – 2α) = – cos 2α = 2sin²α – 1 = 1/8.
Ответ
arccos 1/8.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет