Задача
Равнобедренные треугольники ABC (AB = BC) и
A1B1C1
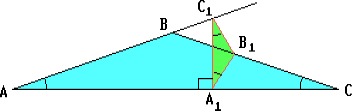
(A1B1 = B1C1) подобны и AC : A1C1 = 5 : 
. Вершины A1 и B1 расположены соответственно на сторонах AC и BC, а вершина C1 – на продолжении стороны AB за точку B, причём A1B1 ⊥ BC. Найдите угол B.
Решение
Пусть A1B1 = B1C1 = 1, ∠C = γ. Тогда
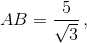∠C1A1C = ∠C1A1B1 + ∠B1A1C = γ + (90° – γ) = 90°, A1C = 1/sin γ, C1A1 = 2cos γ,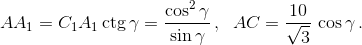 
Поскольку AC = AA1 + A1C, то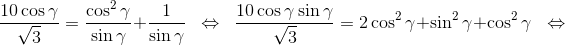 
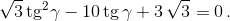
Отсюда tg γ = 
или tg γ = 3 .
Второе решение не удовлетворяет условию: точка C1 лежит на продолжении отрезка AB за точку B, поэтому AB sin γ < A1C1, то есть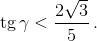 
Следовательно, γ = 30°.
Ответ
120°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет