Задача
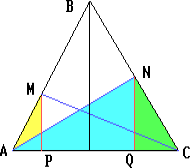
В равнобедренном треугольнике ABC точки M и N находятся на боковых сторонах AB и BC соответственно.
Найдите площадь треугольника ABC, если известно, что AM = 5, AN = 2![]() , CM = 11, CN = 10.
, CM = 11, CN = 10.
Решение
Пусть P и Q – проекции точек M и N на AC. Обозначим AP = x. Тогда из подобия треугольников NQC и MPA получим, что QC = 2x.
NC² – CQ² = AN² – AQ². Отсюда AQ² = 148 + 4x² – 100 = 48 + 4x².
Аналогично CP² = 96 + x². Поскольку CP – AQ = (AC – x) – (AC – 2x) = x, то
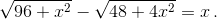
Решив это уравнение, получим x = 2. Значит,
CP = 10, AC = 12, BC = 15. По формуле Герона 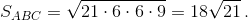
Ответ
18![]() .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет