Задачи и олимпиады по математике

Задача

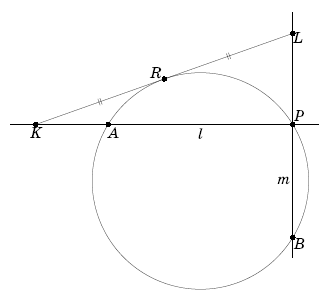
Взаимно перпендикулярные прямые l и m пересекаются в точке P окружности так, что они разбивают окружность на три дуги. Отметим на каждой дуге такую точку, что проведённая через неё касательная к окружности пересекается с прямыми l и m в точках равноотстоящих от точки касания. Докажите, что три отмеченные точки являются вершинами равностороннего треугольника.

Решение

Пусть A и B – точки пересечения прямых l и m с данной окружностью, дуга PA равна 3α, прямая n – касательная в точке R, а K, L – точки пересечения n с l и m соответственно (см. рис.).

ТогдаPR– медиана прямоугольного треугольникаPKL, проведённая к гипотенузе, откуда следует, что оба треугольникаPRKиPRL– равнобедренные. Поскольку ∠LPR= 2∠APR, а эти углы измеряются половинами дугARиPR, то дугаPRсоставляет 2α. Аналогичное рассуждение проходит для дугиPBи лежащей на ней точкиT. Ясно, что в сумме дугиPAиPBсоставляют половину окружности, значит, дугаRTсоставляет треть окружности. Рассуждения для точкиSаналогичны.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления