Решение 1:Пусть M – середина BE. Тогда DM – медиана прямоугольного треугольника EDC, проведённая к гипотенузе EB, поэтому  DM = ½ BE = BM.  Значит,

∠DMA = 2∠MBD = ∠B = ∠A = ∠DAM.  следовательно,  DM = DA = 1,  BE = 2DM = 2.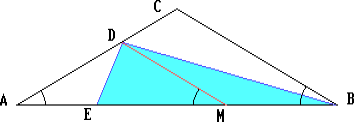

Решение 2:   Пусть прямая ED пересекает прямую ВC в точке F. Тогда в треугольнике EBF биссектриса BD является высотой, следовательно, этот треугольник – равнобедренный:  BE = BF.

  Проведём отрезок DG, параллельный BC (точка G лежит на стороне BC). Так как  ∠DAB = ∠GBA,  то трапеция ADGB – равнобокая:  BG = DC = 1.  DG – средняя линия треугольника BEF. Следовательно,  BE = BF = 2BG = 2.