Задача
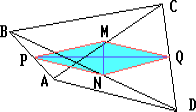
Пусть P и Q – середины сторон AB и CD четырёхугольника ABCD, M и N – середины диагоналей AC и BD.
Докажите, что если MN и PQ перпендикулярны, то BC = AD.
Решение
Поскольку MQ и PN – средние линии треугольников ACD и ABD соответственно, то MQ || PN и MQ = PN. Поэтому четырёхугольник PMQN – параллелограмм, а так как его диагонали перпендикулярны, то это ромб. Следовательно, BC = 2PM = 2PN = AD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет