Решение 1:Пусть  ∠A = α.  Тогда  ∠ACK = 90° – α,  ∠ECK = ∠ACE = 45° – ^α/₂,  ∠KCB = α,  ∠CEB = ∠A + ∠ACE = α + 45° – ^α/₂ = 45° + ^α/₂,

∠BCE = ∠KCB + ∠ECK = α + 45° – ^α/₂ = 45° + ^α/₂.  Следовательно, треугольник CBE равнобедренный и  CB = BE.

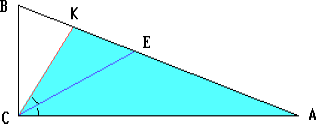
Решение 2:Опустим перпендикуляр EL на AC. Треугольники ECK и ECL равны по гипотенузе и острому углу, поэтому  CK = CL.  Но отрезок CL, очевидно, равен высоте треугольника CBE, опущенной на сторону BC. Следовательно, в треугольнике CBE две высоты равны, то есть он – равнобедренный.

Ответ задачи отсутствует