Задача
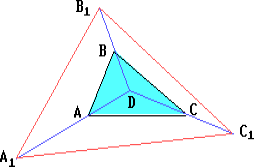
Величины углов при вершинах A, B, C треугольника ABC составляют арифметическую прогрессию с разностью π/7. Биссектрисы этого треугольника пересекаются в точке D. Точки A1, B1, C1 находятся на продолжениях отрезков DA, DB, DC за точки A, B, C соответственно, на одинаковом расстоянии от точки D. Докажите, что величины углов A1, B1, C1 также образуют арифметическую прогрессию. Найдите её разность.
Решение
Пусть ∠A = α – средний по величине угол треугольника ABC, ∠C = α – π/7, ∠B = α + π/7. ∠B1DC1 = π/2 + α/2 (см. задачу 155448),
∠DB1C1 = ∠DC1B1 = ½ (π – π/2 – α/2) = π/4 – α/4. Аналогично ∠DA1C1 = ∠DC1A1 = π/4 – α/4 – π/28, ∠DA1B1 = ∠DB1A1 = π/4 – α/4 + π/28. Значит,
∠A1 = ∠DA1C1 + ∠DA1B1 = π/2 – α/2, ∠B1 = π/2 – α/2 + π/28, ∠C1 = π/2 – α/2 – π/28.
Ответ
π/28.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь