Задача
Найдите сумму углов при вершинах самопересекающейся пятиконечной звезды.
Решение
Обозначим вершины звезды последовательно: A1, A2, A3, A4, A5. Пусть M – точка пересечения отрезков A1A4 и A2A5, а N – отрезков A1A3 и A2A5. Тогда угол A1MN – внешний угол треугольника MA2A4, а угол A1NM – треугольника NA3A5. Поэтому ∠A1MN = ∠A2 + ∠A4, ∠A1NM = ∠A3 + ∠A5. Следовательно,
∠A1 + ∠A2 + ∠A3 + ∠A4 + ∠A5 = ∠A1 + ∠A1MN + ∠A1NM = 180°. 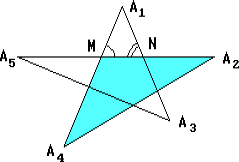
Ответ
180°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет