Первый способ. Отложим на продолжении отрезка AM за точку M отрезок MB₁, равный MB. Пусть прямая KM пересекает отрезок BB₁ в точке P. Тогда

∠BMB₁ = ∠MAB + MBA = ½ (⌣ MB + ⌣MA) = ½ ⌣AKB = ⌣AK = 2∠KMA = 2∠B₁MP.

  Поэтому прямая KP делит угол BMB₁ равнобедренного треугольника BMB₁ пополам. Значит, KP – серединный перпендикуляр к отрезку AB₁. Следовательно,

KB₁ = KB = AK.  Поэтому KH – серединный пенрпедикуляр к отрезку AB₁, и  AH = HB₁ = HM + MB. и   AH = HB₁ = HM + MB.

  Второй способ. Отметим на отрезке AM такую точку B₂, что  AB₂ = MB  (пусть B₂ лежит между точками A и H). Так как точки A и B лежат на окружности по одну сторону от хорды KM, то  ∠KAM = ∠KBM.  Кроме того,  AK = KB,  поэтому треугольники KAB₂ и KBM равны. Значит,  KB₂ = KM  и треугольник B₂KM – равнобедренный. Его высота KH является медианой, поэтому H – середина B₂M. Следовательно,  AH = AB₂ + B₂H = HM + MB.   Третий способ. Пусть луч KH второй раз пересекает окружность в точке L, а прямые AM и LB пересекаются в точке B₁. Вписанные углы ALK и BLK равны, так как каждый из них опирается на половину дуги AKB. Таким образом, высота LH треугольника ALB₁ является его биссектрисой, поэтому треугольник ALB₁ – равнобедренный. Значит,  AH = HB₁  и  ∠MBB₁ = ∠MAL = ∠MB₁B.

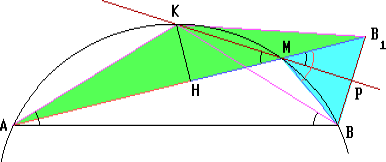
  Поэтому треугольник B₁MB – также равнобедренный и  MB = MB₁.  Следовательно,  AH = HB₁ = HM + MB₁ = HM + MB.

Ответ задачи отсутствует