Задача
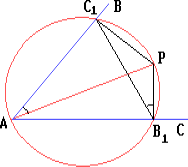
Из точки P, расположенной внутри острого угла BAC, опущены перпендикуляры PC1 и PB1 на прямые AB и AC. Докажите, что ∠C1AP = ∠C1B1P.
Решение
Поскольку отрезок AP виден из точек B1 и C1 под прямым углом, то точки C1 и B1 лежат на окружности с диаметром AP. Следовательно, ∠C1AP = ∠C1B1P как вписанные углы, опирающиеся на одну и ту же дугу.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет