Задача
Докажите, что отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной окружностью пополам.
Решение
Пусть вневписанная окружность касается стороны AB треугольника ABC;
$\displaystyle \angle$C = $\displaystyle \alpha$, $\displaystyle \angle$CAB = $\displaystyle \beta$, $\displaystyle \angle$CBA = $\displaystyle \gamma$;
O1,O2— центры вписанной и вневписанной
окружностей соответственно,M— серединаO1O2.
Поскольку отрезок
O1O2 виден из точек A и B под прямым
углом, то M — центр окружности, описанной около четырёхугольника
AO1BO2. Тогда
$\displaystyle \angle$AO2B = $\displaystyle \angle$AO2O1 + $\displaystyle \angle$BO2O1 = $\displaystyle \angle$O1BA + $\displaystyle \angle$O1AB = $\displaystyle {\frac{\gamma}{2}}$ + $\displaystyle {\frac{\beta}{2}}$ = 90o - $\displaystyle {\frac{\alpha}{2}}$,
$\displaystyle \angle$AMB = 2$\displaystyle \angle$AO2B = 180o - $\displaystyle \alpha$.
Следовательно, точкиA,C,BиMлежат на одной окружности,
т.е. на окружности, описанной около треугольникаABC.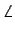
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет