Задача
Существует ли непрерывная функция, принимающая каждое действительное значение ровно 3 раза?
Решение
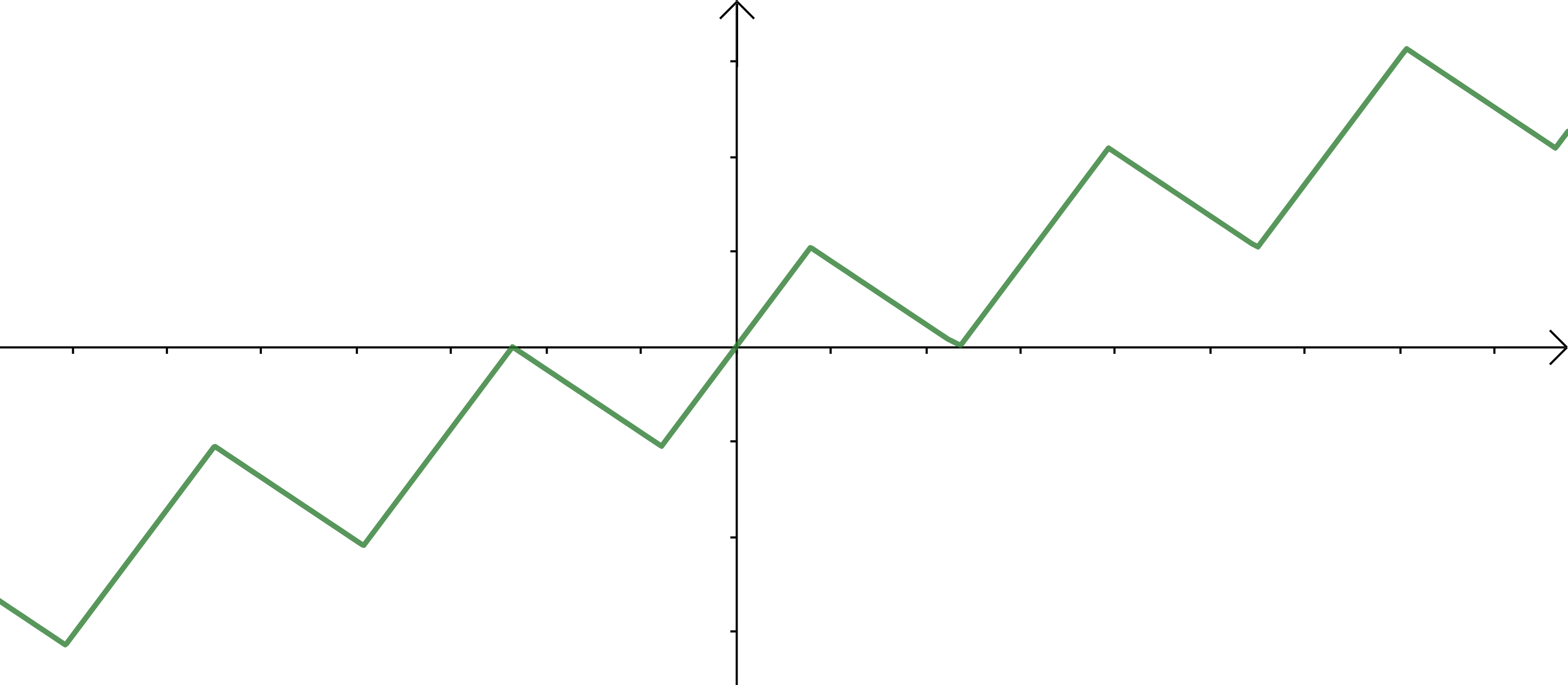
Один из возможных вариантов – функция $f(x) = \frac{x}{3} + \arcsin(\sin x)$,
график которой есть "пила", изображенная на картинке.
Другой вариант - функция
$f(x) = \frac{2x}{3\pi} + \sin x$.
Это пример "сглаженной пилы".
Ответ
существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет