Задача
Цифры 0, 1, ..., 9 разбиты на несколько непересекающихся групп. Из цифр каждой группы составляются всевозможные числа, для записи каждого из которых все цифры группы используются ровно один раз (учитываются и записи, начинающиеся с нуля). Все полученные числа расположили в порядке возрастания и k-му числу поставили в соответствие k-ю букву алфавита АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ. Оказалось, что каждой букве соответствует число и каждому числу соответствует некоторая буква. Шифрование сообщения осуществляется заменой каждой буквы соответствующим ей числом. Если ненулевое число начинается с нуля, то при шифровании этот нуль не выписывается. Восстановите сообщение 873146507381 и укажите таблицу замены букв числами.
Решение
Группу из k цифр будем обозначать Gk. Заметим, что числам, составленным из цифр этой группы, соответствует ровно k! букв. Поскольку в сообщении отсутствуют цифры 2 и 9, эти цифры образуют либо две группы по одной цифре, либо одну группу из двух цифр. В обоих случаях эти цифры могут быть использованы для зашифрования ровно двух букв алфавита. Так как
31 = 1! + 3! + 4!, то множество {1, 3, 4, 5, 6, 8, 0} является объединением множеств G1, G3, G4. Если G1 ≠ {1}, то из сообщения находим:
а) G4 = {1, 3, 7, 8}, G3 = {0, 5, 6}, G1 = {4}, либо
б) G4 = {1, 3, 7, 8}, G3 = {4, 5, 6}, G1 = {0}.
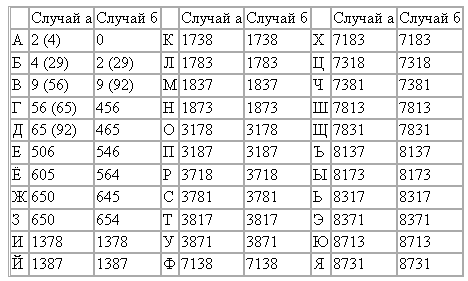
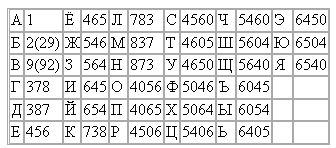
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь