Задачи и олимпиады по математике

Задача

а) 10 точек, делящие окружность на 10 равных дуг, попарно соединены пятью хордами. Обязательно ли среди них найдутся две хорды одинаковой длины?б) 20 точек, делящие окружность на 20 равных дуг, попарно соединены 10 хордами. Докажите, что среди них обязательно найдутся две хорды одинаковой длины?

Решение

а) См. рисунок. Разным дугам соответствуют разные хорды.

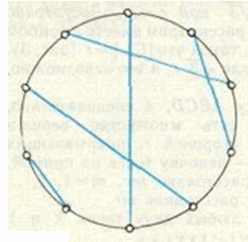
б) Предположим нам это удалось. Будем считать, что длина окружности равна 20. Десяти разным хордам соответствуют десять разных дуг длины 1, 2, ..., 10. Раскрасим точки в синий и красный цвет через одну. Дуги нечётной длины соединяют точки разного цвета, то есть они соединят пять синих и пять красных точек. Оставшиеся дуги чётной длины должны соединять точки одного цвета. Но пять оставшихся красных точек нельзя разбить на пары. Противоречие.

Ответ

а) Не обязательно.

Задача

Решение

Ответ

Подтверждение удаления