Обозначим данные отрезки  I₁, I₂, ... , I_k,  а их длины –  s₁, s₂, ... , s_k.  Рассмотрим семейство T_ij всевозможных отрезков, один конец которых принадлежит I_i, а другой конец – I_j. Минимальная длина такого отрезка равна растоянию l между ближайшими вершинами отрезков, а максимальная –  l + s_i + s_j.  Таким образом, числа, выражающие длины отрезков семейства T_ij, принадлежат отрезку длины  s_i + s_j.  Длины отрезков семейства T_i, оба конца которых принадлежат I_i, заполняют отрезок длины s_i. Отсюда получаем, что числа, выражающие длины всех отрезков с концами в множестве M, заполняют несколько отрезков суммарной длины

С другой стороны, по условию эти числа принимают все значения от 0 до 1; отсюда   k(s₁+s₂+ ... +s_k) ≥ 1,   то есть   s₁+s₂+ ... +s_k≥¹/_k.

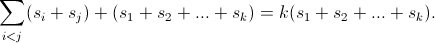
Ответ задачи отсутствует