Задача
Докажите, что площадь проекции куба с ребром 1 на любую плоскость численно равна длине его проекции на прямую, перпендикулярную этой плоскости.
Решение
Будем считать, что плоскость из условия горизонтальна. Обозначим через O самую нижнюю вершину куба, а через A, B, C – соседние с ней вершины. Проекция куба на ось Oz – это проекция на эту ось его большой диагонали, то есть вектора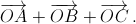 
Она равна cos α + cos β + cos γ, где α, β, γ – углы, которые стороны OA, OB, OC составляют с осью Oz.
Площадь же проекции куба на плоскость xOy равна сумме проекций трёх его нижних граней. Площадь каждой грани, равная 1, при проектировании умножается на соответствующий косинус (угол между плоскостями AOB и xOy равен γ и т. п.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь