Задача
а) Докажите, что число точек пересечения двух замкнутых ломаных на плоскости, находящихся в общем положении, чётно.
б) Верно ли это для замкнутых ломаных, нарисованных на поверхности оконной рамы?
Решение
а) Первая ломаная делит плоскость на несколько областей, причём их можно раскрасить в шахматном порядке (см. решение задачи 197794). Будем двигаться по второй ломаной от одной из вершин. При каждом пересечении с первой ломаной цвет области меняется на противоположный. Поэтому, когда мы вёрнемся в исходную вершину, число пересечений будет чётным. б) См. рис.
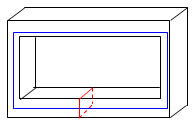
Ответ
б) Неверно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет