Задача
Даны два приведённых квадратных трёхчлена. График одного из них пересекает ось Ox в точках A и M, а ось Oy – в точке C. График другого пересекает ось Ox в точках B и M, а ось Oy – в точке D. (O – начало координат; точки расположены как на рисунке.) Докажите, что треугольники AOC и BOD подобны.
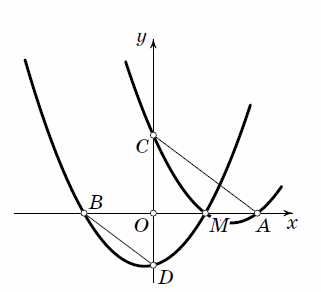
Решение
Обозначим координаты точек: M(x0, 0), A(x1, 0), B(x2, 0). Корни первого трёхчлена равны x0 и x1, корни второго равны x0 и x2. Ордината точки C равна свободному члену первого трёхчлена, то есть x0x1. Аналогично, ордината точки D равна x0x2. Поэтому отношения катетов OC : OA и OD : OB прямоугольных треугольников AOC и BOD равны x0; следовательно, они подобны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет