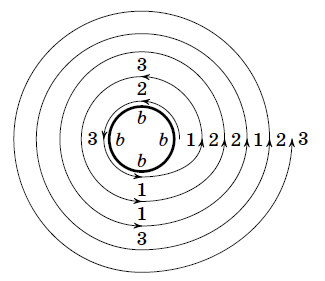
Так как Игорь прошёл целое число кругов, то он встретил первое пирожное в момент подхода к столу. Кроме того, последовательность поедания пирожных не изменится, если убрать требование о "равных промежутках".   Если бы пирожных было четыре, Игорь прошёл бы ровно пять кругов (см. рисунок).

  Пусть число пирожных на столе делится на три. Тогда за первый круг Игорь съедает каждое третье пирожное и возвращается в исходное положение. Таким образом, после одного круга пирожных становится²/₃от того количества, что было на столе. Значит, если бы пирожных было шесть, Игорь прошёл бы ровно шесть кругов, и если бы пирожных было девять, Игорь прошёл бы ровно семь кругов.   Если пирожных больше девяти, то Игорь пройдёт какое-то расстояние до того, как пирожных останется ровно девять, дойдёт до ближайшего пирожного и после этого сделает ровно семь кругов. Значит, всего он прошёл больше семи кругов.   Если же пирожных меньше девяти, a кругов тоже семь, то, как выше, докажем, что для девяти пирожных число кругов больше семи. Противоречие.