Таким числом будет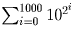. В его десятичной записи единицы стоят в разрядах с номерами 1, 2, 4, 8, …, 2¹ººº (разряды мы считаем справа, то есть разряд единиц имеет номер 1, десятков — 2 и т.д.), а остальные цифры — нули. Сумма цифр числа равна 1001. При возведении этого числа в квадрат мы получим единицы в разрядах с номерами 2²ⁱ(i = 0,1, … ,1000), двойки в разрядах 2^i + j(i,j = 0,1, … ,1000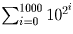) и нули в остальных местах. Сумма цифр этого квадрата равна 1001².

Ответ задачи отсутствует