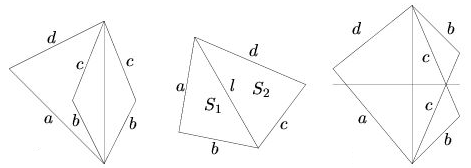
Заметим, что достаточно ограничиться рассмотрением случая выпуклого четырёхугольника. Действительно, для любого невыпуклого четырёхугольника мы можем построить выпуклый с теми же длинами сторон, но большей площади, отразив две его стороны относительно диагонали, лежащей снаружи (рис. слева). Рассмотрим два случая.

  1) Стороны a и b смежны. Разобьём четырёхугольник диагональю на два треугольника со сторонами a, b, l и c, d, l (рис. в центре). Площадь первого не превосходит ^ab/₂, второго – ^cd/₂. Сложив, получим требуемое неравенство.

  2) Стороныaиbне смежны. Разобьём снова данный четырёхугольник на два треугольника диагональю. Треугольник, имеющий стороныaиdоставим на месте, а имеющий стороныbиcотразим относительно серединного перпендикуляра к проведенной диагонали (рис. справа). Получим четырёхугольник с теми же сторонами и той же площади, но стороныaиbуже смежны. А для такого четырёхугольника неравенство уже доказано.

Ответ задачи отсутствует