Задача
Из шахматной доски вырезали одну угловую клетку. На какое наименьшее число равновеликих треугольников можно разрезать эту фигуру?
Решение
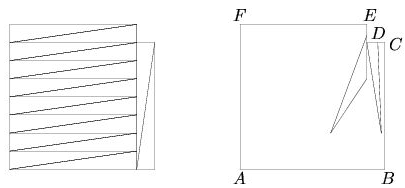
Оценка. Примем за единицу площадь одной клетки. Данная фигура представляет собой невыпуклый шестиугольник ABCDEF площади 63 с углом 270° в вершине D (рис. справа). Если фигура разбита на треугольники, то, очевидно, точка D должна принадлежать по крайней мере двум треугольникам, причём у одного из них сторона лежит на прямой DE, а у другого – на DC. Более того, по крайней мере для одного из них она лежит на соответствующем отрезке. Для определенности предположим, что это треугольник DKL, где K лежит на отрезке DC. Тогда основание DK этого треугольника не больше
DC = 1, а высота – не больше BC = 7. Поэтому SDKL ≤ 7/2. Если все треугольники равновелики, то их не меньше 63 : 7/2 = 18.
Пример разрезания на 18 равновеликих треугольников см. на рис. слева.
Ответ
На 18 треугольников.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь