Задача
a1, a2, a3, a4, a5, a6 – последовательные стороны шестиугольника, все углы которого равны. Докажите, что a1 – a4 = a3 – a6 = a5 – a2.
Решение
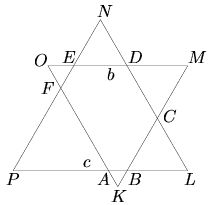
Продолжим стороны данного шестиугольника ABCDEF до пересечения друг с другом. Шестиугольник оказался представленным в виде пересечения двух равносторонних треугольников KMO и LNP (см. рис.) со сторонами b и c соответственно. Объединение этих треугольников представляет собой шестиконечную звезду, лучи которой ABK, BCL, CDM, DEN, EFO и FAP являются равносторонними треугольниками. Следовательно,
b – c = KM – LN = (KB + BC + CM) – (LC + CD + DN) = KB + (BC – LC) + (CM – CD) – DN = a1 + 0 + 0 – a4 = a1 – a4.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет