Искомое геометрическое место середин хорд — это дуга окружности, построенной на отрезке, соединяющем данную точку и центр данной окружности, как на диаметре, лежащая внутри данной окружности (в частности, если точка лежит внутри окружности, то получается вся окружность).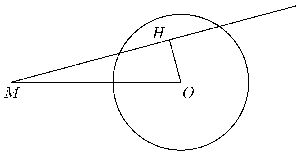Пусть O — центр данной окружности, M — данная точка, l — произвольная прямая, пересекающая окружность и проходящая через точку M, H — середина хорды, получающейся при пересечении прямой окружности (см. рис.). Воспользуемся известной теоремой: радиус перпендикулярен хорде тогда и только тогда, когда он делит ее пополам. Из этой теоремы следует, что угол MHO — прямой. Из обратной теоремы о величине угла, опирающегося на диаметр, следует, что точка H лежит на окружности с диаметром OM. Обратно, пусть H — точка, лежащая на окружности с диаметром OM и внутри данной окружности. По прямой теореме о величине угла, опирающегося на диаметр, получаем, что прямые MH и HO перпендикулярны. Применив теорему о радиусе, перпендикулярном хорде, еще раз, получим, что k — середина хорды, образованной прямой, проходящей через точку M.

Ответ задачи отсутствует