а) Пронумеруем все места за столом по кругу и всех сидящих соответственно занимаемым местам. Будем считать, что нам удалось всех пересадить требуемым образом. Без ограничения общности можно считать, что человек 1 остался сидеть на своем месте. Если это не так, то этого можно добиться поворотом стола; при этом условие задачи нарушиться, очевидно, не может. Человек 2 может сидеть либо на месте 4, либо на месте 13. Разберем первый из этих случаев (рис. a). В этом случае для третьего есть единственное место, удовлетворяющее условию — 7. Далее, 4-й может сидеть только на месте 10, 5-й — на месте 13. При этом для 6-го единственное возможное место — 1. Но оно уже занято первым. Значит, рассадить людей требуемым образом не удастся. Второй случай разбирается аналогично.б) Опять пронумеруем места подряд вокруг стола и людей соответственно занимаемым местам. На рис. б) показан способ пересадить людей, удовлетворяющий условиям задачи.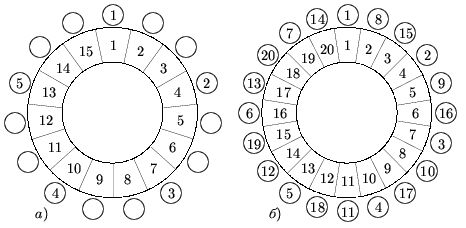

Ответ задачи отсутствует