Решение 1: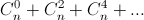   – это количество "чётных" подмножеств множества из n элементов, а  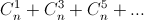    – количество "нечётных" подмножеств. Эти количества равны (см. решение 1 задачи 130711).

Решение 2:Сумма чисел, стоящих на чётных местах в n-й строке треугольника Паскаля, равна сумме чисел, стоящих на нечётных местах той же строки. Действительно, пусть в предыдущей строке стоят числа  c₀, c₁, ..., c_n–1.  Тогда на чётных местах n-й строки стоят числа  c₀,  c₁ + c₂,  c₃ + c₄, ...; их сумма равна

c₀ + c₁ + ... + c_n–1.  А на нечётных местах стоят числа  c₀ + c₁,  c₂ + c₃,  c₄ + c₅, ...  с той же суммой.

Ответ задачи отсутствует