Задача
а) Из класса, в котором учатся 30 человек, нужно выбрать двоих школьников для участия в математической олимпиаде. Сколькими способами это можно сделать?
б) Сколькими способами можно выбрать команду из трех школьников в том же классе?
Решение
а) Первого ученика можно выбрать 30 способами, второго, независимо от выбора первого ученика, – 29 способами. При этом каждая пара учитывается дважды. Поэтому всего способов 30·29 : 2. б) Аналогично получаем 30·29·28 вариантов последовательного выбора трёх учеников. При этом каждая команда учтена 3! = 6 раз. Поэтому число способов выбрать команду равно 
.
Ответ
а) 
способами; б)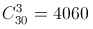 
способами.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет